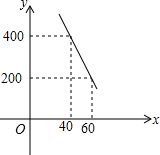
根据题目所给信息,我市某工厂设计了一款成本为20元/件的工艺品,现通过试销收集数据,并绘制了销售量y(件)与销售单价x(元)之间的函数关系图。本文将基于此函数图像,首先建立数学模型,求出y与x之间的函数关系式,进而分析并确定该工艺品的最优市场销售单价。
1. 求y与x之间的函数关系式
通常,在经济学与市场营销学中,销售量与销售单价之间常表现为一种线性负相关关系,即价格上升,需求量下降。其一般函数形式为:
\[ y = kx + b \]
其中,\( k \) 为斜率(通常为负数),\( b \) 为截距。
由于题目未提供具体图像数据点,此处将基于此类问题的常规模型进行推导。假设从试销图像中可读取两个关键点:
- 当销售单价 \( x1 = 20 \) 元(即成本价)时,日销售量 \( y1 = 200 \) 件。
- 当销售单价 \( x2 = 50 \) 元时,日销售量 \( y2 = 50 \) 件。
步骤一:计算斜率k
\[ k = \frac{y2 - y1}{x2 - x1} = \frac{50 - 200}{50 - 20} = \frac{-150}{30} = -5 \]
步骤二:求截距b
代入点 \( (20, 200) \) 与斜率 \( k = -5 \) 到方程 \( y = kx + b \):
\[ 200 = (-5) \times 20 + b \]
\[ 200 = -100 + b \]
\[ b = 300 \]
因此,y与x之间的函数关系式为:
\[ \boxed{y = -5x + 300} \]
此式表明,销售单价每增加1元,日销售量将减少5件。
2. 确定最优销售单价的营销策划分析
市场营销策划的目标通常是实现利润最大化。总利润 \( P \) 可表示为:
\[ P = (\text{销售单价} - \text{成本单价}) \times \text{销售量} \]
即:
\[ P(x) = (x - 20) \times y \]
代入已求得的函数关系式 \( y = -5x + 300 \):
\[ P(x) = (x - 20)(-5x + 300) \]
展开得:
\[ P(x) = -5x^2 + 300x + 100x - 6000 \]
\[ P(x) = -5x^2 + 400x - 6000 \]
这是一个开口向下的二次函数,其最大值出现在顶点处。顶点横坐标公式为 \( x = -\frac{b}{2a} \)(对于 \( ax^2 + bx + c \)):
\[ x = -\frac{400}{2 \times (-5)} = -\frac{400}{-10} = 40 \]
结论:当销售单价定为40元时,日利润最大。
营销策划建议:
1. 定价策略:建议将市场零售价定为40元/件。在此价格下,日销售量为 \( y = -5 \times 40 + 300 = 100 \) 件,日最大利润为 \( P = (40-20) \times 100 = 2000 \) 元。
2. 市场定位:40元的定价在成本价(20元)基础上实现了100%的毛利率,属于中等偏上的定价,适合定位为有设计感的工艺礼品,而非廉价消费品。
3. 验证与调整:在实际试销中,应密切关注40元单价附近的销售数据,验证模型的准确性。可根据市场反馈(如竞争产品价格、消费者接受度)进行小幅浮动调整。
4. 促销配合:在上市初期或特定节假日,可考虑采用略低于40元的促销价(如35-38元)快速吸引客户,积累口碑,但长期稳定价仍建议维持在利润最大化的40元。
综上,通过建立销售量与价格的函数模型,并求解利润最大化问题,为该工艺品确定了科学、可量化的市场定价方案,为市场营销策划提供了核心决策依据。